Colligative Properties
Colligative properties are properties that depend on the concentration of a solute but not on its identity.
Definition: A colligative property may be defined as one which depends on the number of particles in solution and not in any way on the size or chemical nature of the particles.
The four principal colligative properties are
(1) Lowering of the Vapour Pressure
(2) Elevation of the Boiling Point
(3) Depression of the Freezing Point
(4) Osmotic Pressure
The essential feature of these properties is that they depend only on the number of solute particles present in solution. Being closely related to each other through a common explanation,
these have been grouped together under the class name Colligative Properties.
(Greek colligatus = Collected together).
these have been grouped together under the class name Colligative Properties.
(Greek colligatus = Collected together).
Importance
- Molecular mass of substances can be determined.
- Whether a solution is iso-osmotic or not can be found.
- The behavior of solution of electrolytes can be understood.
- The osmotic properties of body fluids such as lacrimal fluids and blood can be evaluated.
- Isotonic solutions can be prepared
Lowering of vapour pressure
Vapor pressure is the pressure of the vapor present. Vapor pressure is caused by molecules that have escaped from the liquid phase to the gaseous phase.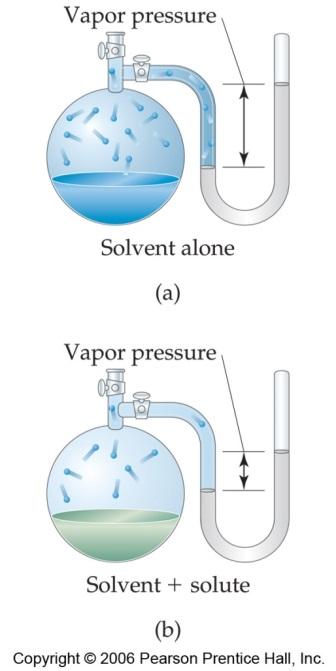
Experiments show that the vapor pressure of a solvent in solution containing a nonvolatile* (*a substance with little tendency to become a gas) solute is always lower than the vapor
pressure of the pure solvent at the same temp. This lowers the freezing point and raises the boiling point.
pressure of the pure solvent at the same temp. This lowers the freezing point and raises the boiling point.
When a nonvolatile solute is dissolved in solution, the presence of solute molecules in the surface blocks a fraction of the surface where no evaporation can take place and fewer particles
enter the gaseous state. This causes the lowering of the vapour pressure. Therefore, the vapor pressure of a solution is lower than that of the pure solvent. The greater the number of
solute particles, the lower the vapor pressure.
enter the gaseous state. This causes the lowering of the vapour pressure. Therefore, the vapor pressure of a solution is lower than that of the pure solvent. The greater the number of
solute particles, the lower the vapor pressure.
Fig. Ions and water molecules interact so that less are able to leave the surface, creating a lower vapor pressure.
Lowering of Vapour Pressure: Raoult’s Law
The vapour pressure of a pure solvent is decreased when a non-volatile solute is dissolved in it.
Raoult (1886) gave an empirical relation connecting the relative lowering of vapour pressure and the concentration of the solute in solution. This is now referred to as the Raoult’s Law.
It states that: the relative lowering of the vapour pressure of a dilute solution is equal to the mole fraction of the solute present in dilute solution.
If p is the vapour pressure of the solvent and ps that of the solution, the lowering of vapour pressure is (p – ps). This lowering of vapour pressure relative to the vapour pressure of the
pure solvent is termed the Relative lowering of Vapour pressure.
pure solvent is termed the Relative lowering of Vapour pressure.
Thus,
Relative Lowering of Vapour Pressure =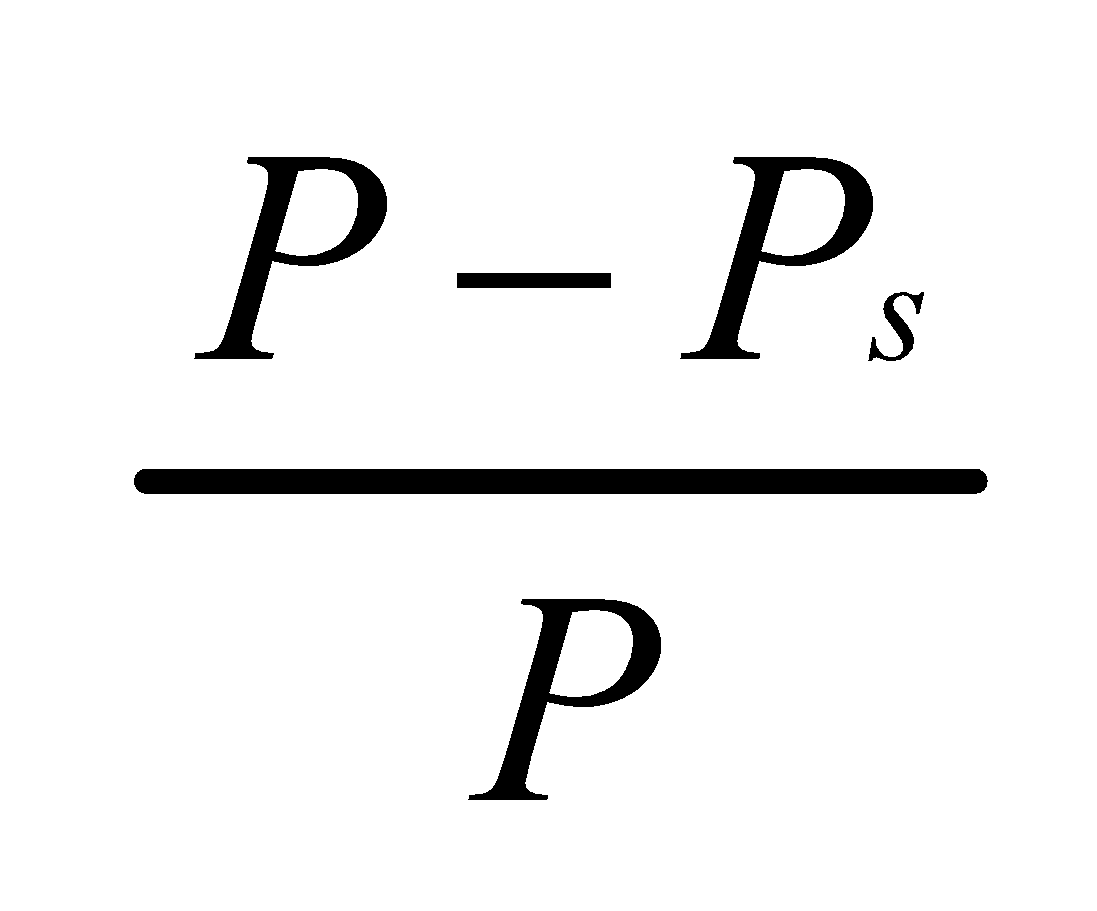
Therefore, Raoult’s Law can be expressed mathematically in the form:
Where n = number of moles or molecules of solute, N = number of moles or molecules of solvent.
Derivation of Raoult’s Law
Let, p is the vapour pressure of the solvent and ps that of the solution,
The vapor pressure of the solution is directly proportional to the mole fraction of the solvent.
The vapor pressure of the solution is, therefore, determined by the number of molecules of the solvent present at any time in the surface which is proportional to the mole fraction.
That is,
The vapor pressure of the solution is, therefore, determined by the number of molecules of the solvent present at any time in the surface which is proportional to the mole fraction.
That is,
Where N = moles of solvent and n = moles of solute.
Where, k =proportionality factor.
In case of pure solvent, n=0 ; And hence mole fraction of solvent 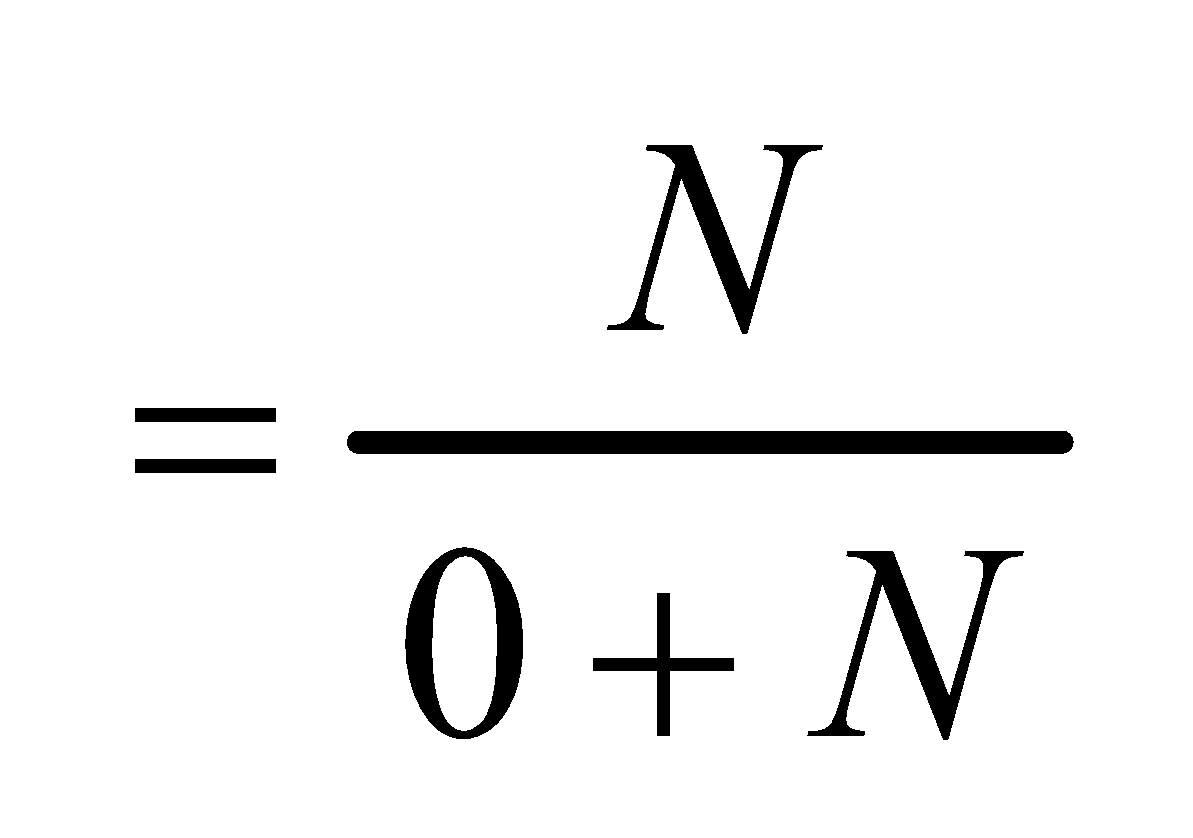


Now from equation (1), the vapor pressure of the solvent p = k
(Since it is a pure solvent it has no solute that means its vapor pressure actually represents the vapor pressure of solvent only.)
Therefore the equation (1) assumes the form
This is Raoult’s Law.
Ideal Solutions and Deviations from Raoult’s Law
A solution which obeys Raoult’s law strictly is called an Ideal solution. A solution which shows deviations from Raoult’s law is called a Nonideal or Real solution.
Suppose the molecules of the solvent and solute are represented by A and B respectively.
Ideal solution. Now let γAB be the attractive force between A and B, and γAA between A and A.
If the solution shows the same vapour pressure then all components have same force of attraction and thus it is an ideal solution. γAB = γAA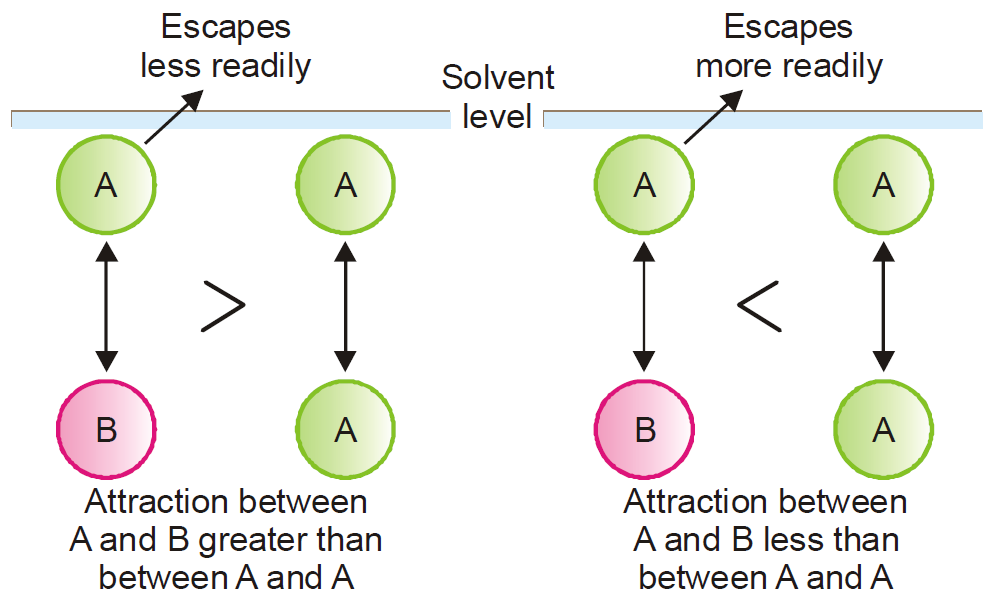
In reality, there are few solutions which obey Raoult’s law strictly. The more dilute a solution the more does it approach ideality. However, if γAB > γAA molecule A will escape less readily
and the vapour pressure will be less than that predicted by Raoult’s law (Negative deviation). On the other hand, if γAB < γAA A molecule will escape from the solution surface more readily
and the vapour pressure of the solution will be higher than predicted by Raoult’s law (Positive deviation).
and the vapour pressure will be less than that predicted by Raoult’s law (Negative deviation). On the other hand, if γAB < γAA A molecule will escape from the solution surface more readily
and the vapour pressure of the solution will be higher than predicted by Raoult’s law (Positive deviation).
Fig. Negative deviation and Positive deviation.
Determination of Molecular Mass from Vapour Pressure Lowering
The molecular mass of a non-volatile solute can be determined by measuring the lowering of vapour pressure (p – ps) produced by dissolving a known weight of it in a known weight of
the solvent. If in a determination w grams of solute is dissolved in W grams of the solvent, m and M are molecular masses of the solute and solvent respectively, we have:
the solvent. If in a determination w grams of solute is dissolved in W grams of the solvent, m and M are molecular masses of the solute and solvent respectively, we have:
No. of Moles of solute 
No. of Moles of solvent
We know that, Raoult’s Law
Substituting these values in the Raoult’s law Equation,
Since for very dilute solution, the number of moles (molecules) of solute (w/m), is very small, it can be neglected in the denominator. The equation (1) can now be written as
Knowing the experimental value of p – ps/p, and the molecular mass of the solvent (M), the molecular weight of solute (m) can be calculated from (1) or (2).
Elevation of Boiling Point
When a liquid is heated, its vapour pressure rises and when it equals the atmospheric pressure, the liquid boils. The addition of a non-volatile solute lowers the vapour pressure and
consequently elevates the boiling point as more heat is needed to supply additional kinetic energy to raise the vapour pressure to atmospheric pressure. It is Called boiling-point elevation.
consequently elevates the boiling point as more heat is needed to supply additional kinetic energy to raise the vapour pressure to atmospheric pressure. It is Called boiling-point elevation.
If Tb is the boiling point of the pure solvent and T is the boiling point of the solution of a nonelectrolyte in that solvent, the difference in the boiling points (ΔTb) is called the elevation of
boiling point: T – Tb = ΔTb
boiling point: T – Tb = ΔTb
For dilute solutions, the curves BD and CE are parallel and straight lines approximately. Therefore for similar triangles ACE and ABD, we have
Where p – p1 and p – p2 are lowering of vapour pressure for solution 1 and solution 2 respectively.
Hence the elevation of boiling point is directly proportional to the lowering of vapour pressure.
or ΔTb ∝ (p – ps).
Fig. The vapour pressure curves of the pure solvent and solutions (1) and (2) with different concentrations of solute (Relationship between Lowering of VP and Elevation of BP)
Raoult’s Law of boiling point elevation
(i) The elevation of boiling point of a solution is proportional to its molal concentration i.e. to its molality, m.
ΔTb = Kb. m where K is known as Boiling point constant, or Ebbulioscopic constant or Molal elevation constant.
When m=1, then Tb = Kb
So, molal elevation constant may be defined as boiling point elevation produced when 1 mole of solute is dissolved in one kg (1000 g) of the solvent.
(ii) Equimolecular quantities of different substances dissolved in the same quantity of a particular solvent raise its boiling point to the same extent.
Depression of Freezing point
The freezing point of a solution is always lower than that of the pure solvent.
The difference of the freezing point of the pure solvent and the solution is referred to as the Depression of freezing point. It is represented by the symbol ΔT or ΔTf .
Tf – T1 = Δ T
Derivation
The vapour pressure curve of a solution (solution 1) of a nonvolatile solute meets the freezing point curve at F, indicating the freezing point of the solution, T1. Adddition of more solute
causes a further lowering of freezing point to T2. Here the freezing point of pure solvent, Tf.
causes a further lowering of freezing point to T2. Here the freezing point of pure solvent, Tf.
For dilute solutions FD and CE are approximately parallel straight lines and BC is also a straight line. Since the triangles BDF and BEC are similar, thus
where p1 and p2 are vapour pressure of solution 1 and solution 2 respectively. Hence depression of freezing point is directly proportional to the lowering of vapour pressure.
or ΔTf ∝ (p – ps).
Raoult’s Law of depression of freezing point
(i) The depression of freezing point of a solution is proportional to its molal concentration i.e. to its molality, m.
ΔTf= Kf. m where Kf is known as molal depression of freezing point constant or cryoscopic constant.
When m=1, then Tb = Kb.
So, cryoscopic constant may be defined as freezing point reduction produced when 1 mole of solute is dissolved in 1000 g of the solvent.
(ii) Equimolecular quantities of different substances dissolved in the same quantity of a particular solvent reduce its freezing point to the same extent.
Osmotic Pressure
The flow of the solvent through a semipermeable membrane from pure solvent to solution or from a dilute solution to concentrated solution is termed osmosis (Greek Osmos means “to
push”.)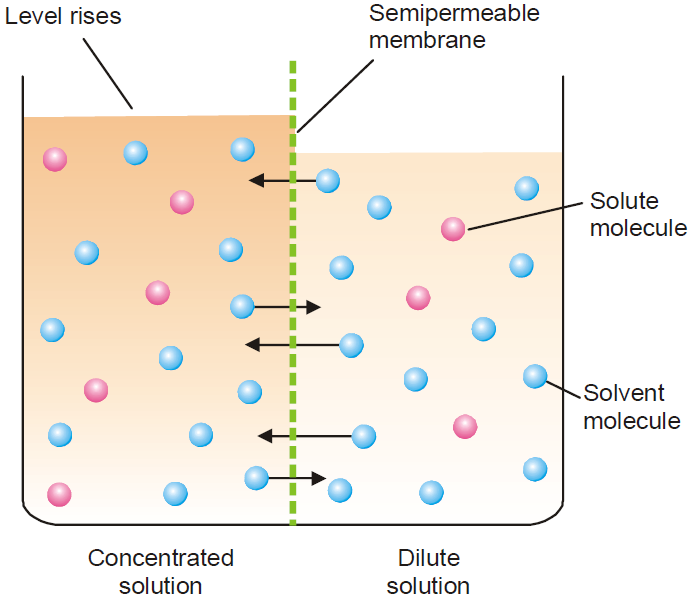
push”.)
Osmotic pressure may be defined as the external pressure applied to the solution in order to stop the osmosis of the solvent into the solution separated by a semipermeable membrane.
A membrane which is permeable to solvent and not to solute is called semipermeable membrane.
Animal and vegetable membranes are not completely semipermeable. Cupric ferrocyanide, Cu2Fe(CN)6, membrane deposited in the walls of porous pot is perfectly a semipermeable
membrane.
membrane.
Van’t Hoff’s Law of Osmotic Pressure
Quantitative relationship between the concentration of the solution and the osmotic pressure was first derived by Van’t Hoff in 1886. These are known as Van’t Hoff’s laws of osmotic
pressure.
pressure.
First Law
The osmotic pressure of a solution at a given temperature is directly proportional to its concentration.
If π is the osmotic pressure and C its concentration in mole/L, we can write π ∝ C, if temperature is constant.
π α C at constant T --------------------------(i)
If V is volume containing one mole of solute, then C=1/V
Thus, π α 1/V at constant T
Or, πV = constant
Second Law
The osmotic pressure of a solution of a given concentration is directly proportional to the absolute temperature.
If T is the absolute temperature, we can write
π ∝ T, if temperature is constant ---------------------------(ii)
Third Law
Equimolecular quantities of different solutes dissolved in such volumes of solvent as to give the same volume of the solution have the same osmotic pressure at the same temperature.
Combining equation (i) and (ii) ---
π α T/V
πV = RT (for one mole of solute/V liter of solution)
πV = nRT (for n mole of solute/V liter of solution)
πV = w/m. RT [w is weight in gm and m is MW]
Determination of MW from Osmotic Pressure
πV = w/m. RT [w is weight in gm and m is MW]
m = wRT/ πV
References
1. A to Z of Thermodynamics Pierre Perrot ISBN 0-19-856556-9
2. Nic, M.; Jirat, J.; Kosata, B., eds. (2006–). "ideal mixture". IUPAC Compendium of Chemical Terminology (Online ed.).
3. P. Atkins and J. de Paula, Atkins’ Physical Chemistry (8th edn, W.H.Freeman 2006), p.144
4. T. Engel and P. Reid Physical Chemistry (Pearson 2006), p.194
5. K.J. Laidler and J.H. Meiser Physical Chemistry (Benjamin-Cummings 1982), p.180
6. S. Berry, S.A. Rice and J. Ross, Physical Chemistry (Wiley 1980) p.750
7. I.M. Klotz, Chemical Thermodynamics (Benjamin 1964) p.322
8. P.A. Rock, Chemical Thermodynamics: Principles and Applications (Macmillan 1969), p.261
Slide Share Link:
Direct download link:
Get the Power Point Slides
Slide Share Link:
Watch Video Tutorials
Software Help
No comments:
Post a Comment