Definition
The study of the flow of heat or any other form of energy into or out of a system as it undergoes a physical or chemical transformation is called Thermodynamics.
Scopes of Thermodynamics
Most of the important laws of Physical Chemistry, including the Van’t Hoff law of lowering of vapour pressure, Phase Rule and the Distribution Law, can be derived from the laws of thermodynamics.
It tells whether a particular physical or chemical change can occur under a given set of conditions of temperature, pressure and concentration.
It also helps in predicting how far a physical or chemical change can proceed, until the equilibrium conditions are established.
Limitations of Thermodynamics
Thermodynamics is applicable to macroscopic systems consisting of matter in bulk and not to microscopic systems of individual atoms or molecules. It ignores the internal structure of atoms and molecules.
Thermodynamics does not bother about the time factor. That is, it does not tell anything regarding the rate of a physical change or a chemical reaction. It is concerned only with the initial and the final states of the
system. It does not give any information about how the final condition is attained or how long it takes to reach this condition.
Thermodynamic Terms and Basic Concepts
An important part of the study of thermodynamics is the following terms and definitions.
System & Surroundings
A system is that part of the universe which is under thermodynamic study and the rest of the universe is surroundings.
Boundary
The real or imaginary surface separating the system from the surroundings is called the boundary.
Fig: Thermodynamic system. Fig: Water contained in a beaker constitutes a system.
Homogeneous Systems
When a system is uniform throughout, it is called a Homogeneous System. Examples are: a pure single solid, liquid or gas, mixtures of gases, and true solution of a solid in a liquid. A homogeneous
system is made of one phase only.
Heterogeneous Systems
A heterogeneous system is one which consists of two or more phases. In other words it is not uniform throughout. Examples of heterogeneous systems are: ice in contact with water, ice in contact with
vapour etc. Here ice, water and vapour constitute separate phases.
Types of Thermodynamic Systems
There are three types of thermodynamic systems depending on the nature of the boundary.
Isolated System
Closed System
Open System
Fig. Three types of thermodynamic systems.
Isolated System: An isolated system is one that can transfer neither matter nor energy to and from its surroundings. Here the boundary is both sealed and insulated; no interaction is possible with the
surroundings. Ex. boiling water, contained in a thermos flask.
Closed System: A closed system is one which cannot transfer matter but can transfer energy in the form of heat, work and radiation to and from its surroundings. Here the boundary is sealed but not
insulated. Ex. A gas contained in a cylinder fitted with a piston
Open System: An open system is one which can transfer both energy and matter to and from its surroundings. In such a system the boundary is open and un-insulated. Ex. Hot water contained in a
beaker placed on laboratory table.
Example
Differences between individual types of chemical systems may be demonstrated using the example of making coffee. The pot on the heater represents a (practically) closed system until the water is
brought to the boil. At the boiling point, when steam is leaking from the pot, it becomes an open system.
The ready-made coffee kept in a thermos bottle represents a simple model of an isolated system.
What are Adiabatic Systems?
Those system in which no thermal energy passes into or out of the system, are said to be adiabatic systems.
Properties
The macroscopic or bulk properties of a system (volume, pressure, mass, etc.) can be divided into two classes:
(a) Intensive properties
(b) Extensive properties
Intensive Properties
A property which does not depend on the quantity of matter (mass) present in the system is known as Intensive Property. Some examples of intensive properties are pressure, temperature, density, and
concentration.
Extensive Properties
A property that does depend on the quantity (the size or extent) of matter present in the system is called an Extensive Property. Some examples of extensive properties are volume, number of moles,
enthalpy, entropy, Gibbs’ free energy, Mass, Volume, Work, Entropy, Enthalpy, Surface area, Internal energy etc.
States
Equilibrium states
A system in which the state variables have constant values throughout the system is said to be in a state of thermodynamic equilibrium. e.g. Constant values of P,V,T of a gas.
Non–Equilibrium states
A system in which the state variables have different values in different parts of the system is said to be in a non-equilibrium state.
Thermodynamic Processes
When a thermodynamic system changes from one state to another, the operation is called a Process. These processes involve the change of conditions (temperature, pressure and volume).

The various types of thermodynamic processes are:
Isothermal Processes
Adiabatic Processes
Isobaric Processes
Isochoric Processes
Cyclic Process
Fig. Four basic thermodynamic processes Fig. cyclic process.
1) Isothermal Processes: Those processes in which the temperature remain fixed or constant, are termed as isothermal processes. For an isothermal process dT = 0
e.g. a constant temperature bath
2) Adiabatic Processes: Those processes in which no heat can flow, into or out of the system are called adiabatic processes. For an adiabatic process dq = 0
e.g. thermos bottle
3) Isobaric Processes: Those processes which take place at constant pressure are called isobaric processes. For an isobaric process dp = 0
e.g. heating of water to its boiling point
4) Isochoric Processes: Those processes in which the volume remains constant are known as isochoric processes. For isochoric processes, dV = 0
e.g. heating of a substance in a non-expanding chamber
5) Cyclic Process: When a system in a given state goes through a number of different processes and finally returns to its initial state, the overall process is called a cycle or cyclic process.
For a cyclic process dE = 0, dH = 0.
Reversible & Irreversible Processes
Reversible process: A thermodynamic reverse process is one that takes place infinitesimally slowly and its direction at any point can be reversed by an infinitesimal change in the state of the system.
Irreversible process: When a process goes from the initial to the final state in a single step and cannot be carried in the reverse order, it is said to be an irreversible process.
Fig. Reversible expansion occurs by decreasing the pressure on the piston by infinitesimal amounts. Irreversible expansion occurs by sudden decrease of pressure from P to Pʹ ʹ, when the gas expands rapidly in a single operation.
Differences between Reversible & Irreversible processes
Reversible Process
|
Irreversible Process
|
1. It takes place in infinite number of infinitesimally small steps and it would take infinite time to occur.
2. It is imaginary as it assumes the presence of frictionless and weightless piston.
3. It is in equilibrium state at all stages of the operation.
4. All changes are reversed when the process is carried out in reversible direction.
5. It is extremely slow.
6. Work done by a reversible process is greater than the corresponding irreversible process.
|
1. It takes place in a finite time.
2. It is real and can be performed actually.
3. It is in equilibrium state only at the initial and final stages of the operation.
4. After this type of process has occurred all changes do not return to the initial state by
themselves.
5. It proceeds at a measureable speed.
6. Work done by an irreversible process is smaller than the corresponding reversible process.
|
Work, energy and heat.
We shall refer the term ‘work’ for mechanical work which is defined as force × distance.
Work is energy in the form of orderly motion, which may, in principle, be harnessed so as to raise a weight. The most common forms of work are pressure-volume work and electrical work. The work done by a system against a constant external
pressure is given by w=−pexΔV. The maximum amount of volume expansion work which a system may accomplish under reversible conditions is given by w=−nRTln(Vf/Vi).
Thermodynamics is a macroscopic science, and at its most fundamental level, is the study of two physical quantities, energy and entropy. Energy may be regarded as the capacity to do work, whilst entropy may be regarded as a measure of the
disorder of a system.
Internal energy
A fundamental parameter in thermodynamics is the internal energy denoted as U or ΔE.
The total of all the possible kinds of energy (kinetic and potential energy) of a system is called its Internal Energy.
In thermodynamics we are concerned only with the energy changes when a system changes from one state to another. If Δ E be the difference of energy of the initial state (Ein) and the final state (Ef),
we can write
ΔE = Ef – Ein
ΔE is +ve if Ef is greater than Ein and –ve if Ef is less than Ein.
A system may transfer energy to or from the surroundings as heat or as work, or both.
Units of Internal Energy
The SI unit for internal energy of a system is the joule (J). Another unit of energy which is not an SI unit is the calorie, 1 cal = 4.184 J.
The first law: In other words, energy may be lost from a system in only two ways, either as work or as heat. As a result of this, it is possible to describe a change in the total internal energy as the sum of energy lost or gained as work and heat,
since U cannot change in any other way. Thus, for a finite change: ΔU=q+w Where q is the heat supplied to the system, and w is the work done on the system. As with ΔU, q and w are positive if energy is gained by the system as heat and work
respectively, and negative if energy is lost from the system as heat or work.
First Law of Thermodynamics
The first law of thermodynamics is, in fact, an application of the broad principle known as the Law of Conservation of Energy to the thermodynamic system. 
It states that: “The total energy of an isolated system remains constant though it may change from one form to another’’.
Explanation: When a system is changed from state A to state B, it undergoes a change in the internal energy from EA to EB.
Thus, we can write
ΔE = EB – EA
This energy change is brought about by the evolution or absorption of heat and/or by work being done by the system. Because the total energy of the system must remain constant, we can write the
mathematical statement of the First Law as :
Where q = the amount of heat supplied to the system
w = work done by the system
Fig. Illustration of First Law. Heat adds to internal energy, while work subtracts.
Thus First Law may also be stated as: the net energy change of a closed system is equal to the heat transferred to the system minus the work done by the system.
As the gas expands against an applied constant pressure, P, by volume ΔV. The total mechanical work done is given by the relation
w = P × ΔV………………………………………………...(2)
From (1) and (2), we can restate
ΔE = q – P × ΔV
Work of Expansion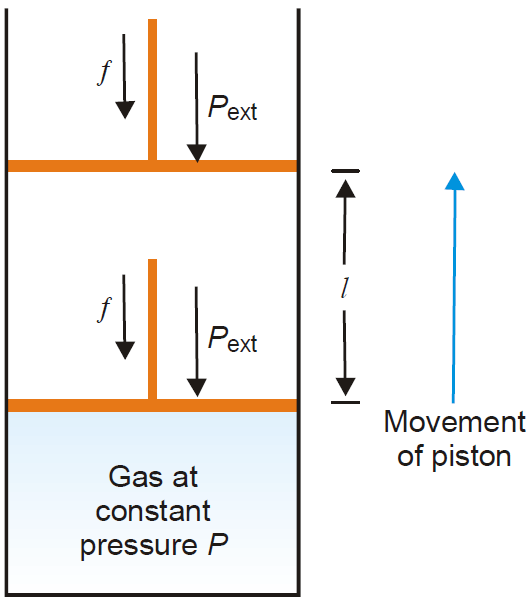
In elementary thermodynamics the only type of work generally considered is the work done in expansion (or compression) of a gas. This is known as pressure-volume work or PV work or expansion
work.
Derivation: Let us consider, a gas contained in a cylinder fitted with a frictionless piston. The pressure (force per unit area) of the gas, P, exerts a force on the piston. This can be balanced by applying an
equal but opposite pressure from outside on the piston.
Let it be designated as Pext.
It is important to remember that it is the external pressure, Pext and not the internal pressure of the gas itself which is used in evaluating work. This is true whether it be expansion or contraction.
Fig. Pressure volume work of a system (gas) confined by a frictionless piston.
If the gas expands at constant pressure, the piston would move, say through a distance l. We know that work = force × distance (by definition)
or w = f × l …………………………….(1)
Since pressure is force per unit area,
f = Pext × A ………………………..(2)
Where A is the cross-section area of the piston.
From (1) and (2), we have
w = Pext × A × l
= Pext × ΔV
Where ΔV is the increase in volume of the gas.
Since the system (here-gas) is doing work on the surroundings (piston), it bears negative sign.
Thus,w = –Pext × ΔV
The work done in compression of a gas can also be calculated. In that case the piston will move down and sign of the work will be positive.
That is, w = Pext × ΔV
Isothermal Reversible Expansion Work of an Ideal Gas
Let us consider an ideal gas confined in a cylinder, fitted with a frictionless and weightless piston. Suppose, the cylinder itself is placed in a heat reservoir of constant temperature T. 
Let, the pressure on the piston is P and the initial volume of the gas is V. If the pressure is decreased by an infinitesimally small amount dP to a value of P-dP, than the volume of the gas at this pressure
increases by an amount dV.
The opposing pressure ( Pext ) is slightly less than pressure of gas (P) hence, Pext = P — dP
Suppose gas expand by a small volume dV, then work done dW Is given by
dW = — Pext × dV
= — (P — dP) × dV
= — P.dV + dP . dV
dP . dV isvery small hence neglected
dW = — P.dV Fig. Isothermal reversible expansion work.
As temperature is maintained constant, the work done in this infinitesimally small change is given by-
W = (P-dP)dV
=P.dV-dP.dV
As the product dP.dV is very small, we can neglect it and write-
W = P.dV…………………(1)
Again if the pressure is decreased by an amount ⎯dP and the volume will increase by ⎯dV and a small amount of work given by equation (1) is done. The total work done in expanding the gas from
initial volume, V1 to the final volume, V2 may be expressed by the integration-
Where, P is the pressure of gas at any instant. The integration may be performed only if a relation exists between the pressure of the gas and volume it occupies.
For 1 mole of an ideal gas PV = RT or, P = RT/V. Since in this process the temperature remains constant we can write,
As P1V1=P2V2, the equation (2) can also be written in the form,
This work done is the maximum possible for the given increase in volume as can be shown in the following manner:-
It is known that ln(1+x) ⋍ x when x is small so that when P1-P2 is small compared to P2 then,
So the equation (3) becomes:
Isothermal Irreversible Expansion Work of an Ideal Gas
Suppose, we have an ideal gas contained in a cylinder with a piston. This time the process of expansion of the gas is performed irreversibly i.e., by instantaneously dropping the external pressure, Pext, to
the final pressure P2. The gas is allowed to expand from a volume V1 to the final volume, V2 then the work done by the system is given by the following expression:
= P2(V2 – V1)
= P2V2 – P2V1
= P2V2 – P1V1+ P1V1 – P2V1
= P2V2 – P2V2+ (P1 – P2 )V1 ( As P1V1 =P2V2 )
= 0+ (P1 – P2 )V1
 [For 1 mole of ideal gas] ……………………………(4)
[For 1 mole of ideal gas] ……………………………(4)
Comparing the equations (3) and (4) we find that, as P1˃P2, Wrev must be larger than Wirr. So, if in an expansion process, a part is irreversible then the work done will be less than the process that was
carried out completely reversibly. In other words, the work done in a reversible process is maximum.
Enthalpy of a System
Enthalpy H (from the Greek word enthalpien, which means to heat) is a property and is defined as the sum of the internal energy E and the PV product.
In order to study the heat changes for reactions taking place at constant pressure and constant temperature, chemists have introduced a new term called enthalpy and is represented by the symbol H.
The enthalpy of a system is defined as the sum of the internal energy and the product of its pressure and volume. That is,
H = E + PV…………………………………………………………………………..(1)
Where E is the internal energy, P is the pressure and V is the volume of the system.
It is also called Heat content.
Change in Enthalpy
If Δ H be the difference of enthalpy of a system from the initial state (H1) to the final state (H2)
Then, ΔH = H2 – H1 ……………………………………………………………………………...(2)
Substituting the values of H2 and H1, as from (1) and (2), we have
ΔH = (E2 + P2V2) – (E1 + P1V1)
= (E2 – E1) + (P2V2 – P1V1)
= ΔE + ΔPV
If P is constant while the gas is expanding, we can write
ΔH = ΔE + PΔV
or ΔH = ΔE + w (w = work) ……………………………………………………...(3)
According to the First Law,
ΔE = q – w ………………………………………………………………………..(4)
where q = heat transferred
From equations (3) and (4)
ΔH = q when change in state occurs at constant pressure
This relationship is usually written as
ΔH = qp
Where subscript p means constant pressure.
Thus Δ H can be measured by measuring the heat of a process occurring at constant pressure.
Molar Heat Capacities
Heat capacity of a system is the heat absorbed by unit mass in raising the temperature by one degree (K or º C) at a specified temperature.
If ‘q’ calories is the heat absorbed by mass ‘m’ and the temperature rises from T1 to T2, the heat capacity (c) is given by the expression-
When mass considered is 1 mole, the expression (1) can be written as
Where C is denoted as Molar heat capacity.
The molar heat capacity of a system is defined as the amount of heat required to raise the temperature of one mole of the substance (system) by 1 K.
Since the heat capacity (C) varies with temperature; its true value will be given as
Where dq is a small quantity of heat absorbed by the system, producing a small temperature rise dT.
Thus the molar heat capacity may be defined as the ratio of the amount of heat absorbed to the rise in temperature.
Units of Heat Capacity
The usual units of the molar heat capacity are calories per degree per mole (cal K–1mol–1), or joules per degree per mole (J K–1mol–1), the latter being the SI unit.
Types
The two important types of molar heat capacities are those: (1) at constant volume; and (2) at constant pressure.
Molar Heat Capacity at Constant Volume
According to the first law of thermodynamics
dq=dE+PdV-------------------------------------------------------(1)
Dividing the both sides of the eq. (1) by dT, we have
At constant volume dV = 0, the equation reduces to
Thus the heat capacity at constant volume is defined as the rate of change of internal energy with temperature at constant volume.
Molar Heat Capacity at Constant Pressure
Equation (ii) above may be written as
We know H = E + PV
A small change in the enthalpy can be expressed as
dH=dE+dPV
Now differentiating this equation w.r.t T at constant pressure, we get
Comparing the eq. (4) with (3) we have
Thus heat capacity at constant pressure is defined as the rate of change of enthalpy with temperature at constant pressure.
JOULE-THOMSON EFFECT
Joule and Thomson (later Lord Kelvin) showed that when a compressed gas is forced through a porous plug into a region of low pressure, there is appreciable cooling.
The phenomenon of producing lowering of temperature when a gas is made to expand adiabatically from a region of high pressure into a region of low pressure is known as Joule-Thomson Effect or
Joule-Kelvin Effect.
Adiabatic Expansion of an Ideal Gas
A process carried in a vessel whose walls are perfectly insulated so that no heat can pass through them, is said to be adiabatic. In such a process there is no heat exchange between a system and
surroundings, and q = 0.
According to the First law
ΔE = q – w = 0 – w
Or, ΔE = – w ……………………………………..(1)
Since the work is done at the expense of internal energy, the internal energy decreases and the temperature fall.
Prove that, PVγ=Constant
Let us consider that, one mole of an ideal gas is confined ina cylinder, fitted with a frictionless piston at a pressure,P; Volume,V; Temperature, T; with the Internal energy, E.
Now let, dq amount of heat is transferred to the system, thus the pressure, volume, temperature and internal energy to dP,dV,dT and dE.
According to the first law of thermodynamics know,
dE=dq-dw
Or, dE=dq –PdV---------------------------------------------(1)
In an adiabetic process there is no heat exchange between a system and surroundings, and dq = 0.
Accordingly the equation (1) becomes
Or, dE=0–PdV
Or, dE=–PdV---------------------------------------------(2)
By definition, Molar heat capacity at constant volume,
Or, dE=CvdT---------------------------------------(3)
From the equation and 2 and 3 we get,
CvdT=–PdV--------------------------------------(4)
For one mole of an ideal gas
PV=RT
Putting the value of P in the equation 4 we get,
Integrating the equation 5, from T1 to T2 and V1 to V2 considering Cv constant, we get,
Or,P1V1γ =P2V2γ
Or, PVγ =Constant.
Joule-Thomson Experiment
The apparatus used by Joule and Thomson to measure the temperature change on expansion of a given volume of gas is illustrated in Fig. An insulated tube is fitted with a porous plug in the middle and
two frictionless pistons A and B on the sides. Let a volume V1 of a gas at pressure P1 be forced through the porous plug by a slow movement of piston A. The gas in the right-hand chamber is allowed to
expand to volume V2 and pressure P2 by moving the piston B outward. The change in temperature is found by taking readings on the two thermometers.

Joule-Thomson experiment.
Most gases were found to undergo cooling on expansion through the porous plug. Hydrogen and helium were exceptions as these gases showed a warming up instead of cooling.
Explanation: The work done on the gas at the piston A is P1V1 and the work done by the gas at the piston B is P2V2. Hence the net work (w) done by the gas is
w = P2V2 – P1V1
ΔE = q – w (First Law)
But the process is adiabatic and, therefore, q = 0
So, ΔE = E2 – E1 = – w = – (P2V2 – P1V1)
or, E2 – E1 = – (P2V2 – P1V1)
Rearranging,
E2 + P2V2 = E1 + P1V1
H2 = H1 or ΔH = 0
Thus the process in Joule-Thomson experiment takes place at constant enthalpy.
Thermochemistry
In the form of heat (thermal energy) is generally evolved or absorbed as a result of a chemical change.
Definition: Thermochemistry is the branch of physical chemistry which deals with the thermal or heat changes caused by chemical reactions.
Thus thermochemistry provides useful information regarding the bond energies.
Heat of Reaction or Enthalpy of Reaction
The heat of a reaction may be defined as the amount of heat absorbed or evolved when the reaction has taken place at constant pressure or at constant volume between the reactants.
In simple word, the amount of heat absorbed or evolved in a chemical reaction is the heat of reaction.
It is also called Entalpy(H).
ΔH = Hproducts – Hreactants
= Hp – Hr
The value of ΔH may be either zero, negative or positive.
For example,
CO(g) + 1/2 O2(g) → CO2(g) ΔH = – 284.5 kJ.
TYPES OF HEAT (ENTHALPY) OF REACTION
Exothermic reactions: The reactions which are accompanied by the evolution of heat energy are called exothermic reactions.
For an exothermic reaction Hp < Hr and ΔH = – ve,
Endothermic reactions: The reactions which are accompanied by absorption of heat are called endothermic reactions.
For an endothermic reaction Hp > Hr and ΔH = +ve.
Various Heats (Enthalpy) of Reaction
Heat of Formation
The heat of formation of a compound is defined as: The change in enthalpy that takes place when one mole of the compound is formed from its elements.
Standard Heat of Formation
The standard heat of formation of a compound is defined as: The change in enthalpy that takes place when one mole of a compound is formed from its elements, all substances being in their standard states
(298 K and 1 atm pressure).
Heat of Combustion
The heat of combustion of a substance is defined as: the change in enthalpy of a system when one mole of the substance is completely burnt in excess of air or oxygen.
Heat of Solution
Heat changes are usually observed when a substance is dissolved in a solvent. When a reaction takes place in solution, the heat of solution of reactants and products must be taken into consideration.
The heat of solution is defined as: the change in enthalpy when one mole of a substance is dissolved in a specified quantity of solvent at a given temperature.
Heat of Neutralisation
The heat of neutralisation is defined as: the change in heat content (enthalpy) of the system when one gram equivalent of an acid is neutralised by one gram equivalent of a base or vice versa in dilute solution.
Heat of Fusion
It is defined as: the heat change (or enthalpy change) when one mole of a solid substance is converted into the liquid state at its melting point.
Heat of Vapourisation
The heat of vapourisation is defined as : the heat change (or enthalpy change) when one mole of liquid is converted into vapour or gaseous state at its boiling point.
Heat of Sublimation
Sublimation is a process when a solid changes directly into gaseous state without changing into liquid state. It occurs at a temperature below the melting point of the solid.
Heat of sublimation is defined as : the heat change (or enthalpy change) when one mole of a solid is directly converted into the gaseous state at a temperature below its melting point.
Heat of Transition
The heat of transition is defined as: the change in enthalpy which occurs when one mole of an element changes from one allotropic form to another.
Hess’s Law of Constant Heat Summation
We know that, heat changes in chemical reactions are equal to the difference in internal energy (ΔE) or heat content (ΔH) of the products and reactants.
Since ΔE and ΔH are functions of the state of the system, it depends only on the initial and final states of the system and not the manner or the steps in which the change takes place. This generalisation
is known as Hess’s Law.
Statement: If a chemical change can be made to take place in two or more different ways whether in one step or two or more steps, the amount of total heat change is same no matter by which method
the change is brought about.
Explanation: Let us suppose that a substance A can be changed to Z directly.
A → Z + Q1 ΔH1 = – Q1
Where, Q1 is the heat evolved in the direct change. When the same change is brought about in stages:
A → B + q1 ΔH2 = – q1
B → C + q2 ΔH2 = – q2
C → Z + q3 ΔH2 = – q3
Here, the total evolution of heat = q1 + q2 + q3 = Q2
According to Hess’s law Q1 = Q2.
Fig. Illustration of Hess’s Law
Example:
Burning of carbon to CO2: Carbon can be burnt to carbon dioxide directly or it may first be changed to carbon monoxide which may then be oxidised to carbon dioxide.
1st way :
C(s) + O2(g) → CO2(g) ΔH = – 94.05 kcal
2nd way :
C(s) + 1/2 O(g) → CO2(g) ΔH = – 26.42 kcal
CO(g) + 1/2 O2(g) → CO(g) ΔH = – 67.71 kcal

Overall change C(s) + O2(g) → CO2(g) ΔH = – 94.13 kcal
Applications of Hess’s Law
(1) Determination of heat of formation of substances which otherwise cannot be measured experimentally.
(2) Determination of Heat of Transition.
(3) Determination of heats of various reactions.
PROCESSES
Types: There are 2 types of processes
1. Spontaneous or natural process
A process which proceeds of its own accord, without any outside assistance, is termed a spontaneous or natural process.
2. Nonspontaneous or unnatural process
The reverse of spontaneous process which does not proceed on its own, is referred to as a nonspontaneous or unnatural process.
Spontaneity: In general, the tendency of a process to occur naturally is called the spontaneity.
Examples of Spontaneous & Nonspontaneous Processes
Cliff Jumping and Mountain Climbing: Cliff jumping is a spontaneous process, whereas mountain climbing requires work.
Heat Flow: When two balls of metal, one hot and one cold, are connected, heat flows spontaneously from the hot ball to the cold one, never from cold to hot. It requires work to transfer heat
from one place to the other, say, by means of refrigerator pump.
Gas Flow: When a vessel containing a gas is connected to another evacuated vessel, the gas spreads throughout spontaneously unless the pressure is the same in both the vessels. The reverse
process of compressing the gas into the original vessel cannot occur unless work is done on it.
Spontaneous vs Nonspontaneous
ENTROPY
DEFINITION OF ENTROPY
Entropy is a thermodynamic state quantity that is a measure of the randomness or disorder of the molecules of the system.
The symbol of entropy is S, while the change in disorder accompanying a process from start to completion is represented by ΔS and is given by the equation,
ΔS = Sfinal – Sinitial
When Sfinal > Sinitial, ΔS is positive.
Explanation: A process accompanied by an increase in entropy tends to be spontaneous.
Let us consider a molecular system in states A and B (Fig.). In state A all the molecules are arranged and highly ordered, while in state B the molecules are present at random and it is highly disordered.
Figure :(a) State A is highly ordered, low entropy and less probable; (b) State B is highly disordered high entropy and more probable.
(1) By definition, the entropy of A is low and that of B high. Thus an increase of entropy occurs in the change from A to B.
(2) According to the law of chance (probability), A is less probable and B is more probable. Therefore, the change from A to B is spontaneous.
(3) From (1) and (2), it follows that the change from A to B which is accompanied by increase of entropy will tend to be spontaneous.
Hence we can say, in general, that a change in a system which is accompanied by an increase in entropy, tends to be spontaneous.
THE SECOND LAW OF THERMODYNAMICS
Statement:
The second law of thermodynamics states that: whenever a spontaneous process takes place, it is accompanied by an increase in the total energy of the universe.
Explanation: Here more specifically, the term ‘universe’ has taken to mean the system and the surroundings.
Thus,
ΔSuniv = ΔSsyst + ΔSsurr
The second law,tells us that when an irreversible spontaneous process occurs, the entropy of the system and the surroundings increases. In other words ΔSuniv > 0. When a reversible process occurs, the
entropy of the system remains constant. ΔSuniv = 0.
Since the entire universe is undergoing spontaneous change, the second law can be most generally and concisely stated as: the entropy of the system is constantly increasing.
THE THIRD LAW
Statement of the Third Law
All substances in their normal crystalline state at absolute zero, would be the most ordered
sate with zero entropy.
Explanation:
The entropy of a substance varies directly with temperature. For example, water above 100ºC at one atmosphere exists as a gas and has higher entropy (higher disorder). When the system is cooled, the
water vapour condenses to form a liquid. Thus the entropy of the system has decreased. On further cooling, water molecules join together to form ice crystal which are highly ordered and entropy of the
system is very low.
If we cool the solid crystal still further, the vibration of molecules held in the crystal lattice gets slower and they have very little freedom of movement (very little disorder) and hence very small entropy.
Finally, at absolute zero all molecular vibration ceases and water molecules are in perfect order.
Now the entropy of the system will be zero.
This leads us to the statement of the third law of thermodynamics: at absolute zero, the entropy of a pure crystal is also zero. That is, S = 0 at T = 0 K.
Fig. Molecular states in a solid crystal (Illustration of the Third law).
Heat Engines
The flow of heat from a hotter body to a colder body is spontaneous process. The heat that flows out spontaneously can be used to do work with the help of a suitable device. A machine which can do
work by using heat that flows out spontaneously from a high-temperature source to a low-temperature sink, is called a heat engine.
A heat engine takes heat energy from a high-temperature reservoir and converts some of it into work, returning the unconverted heat to a low-temperature sink. A basic heat engine is illustrated in Fig.
A steam engine is a typical heat engine. It takes heat from the boiler (high-temperature source), converts some heat to work and returns the unused heat to the surroundings (low-temperature sink). A
heat engine running on a periodic cyclic process can yield work continuously. Fig. Principle of heat engine (illustration).

Efficiency of a Heat Engine
The ratio of the work obtained in a cyclic process (w) to the taken from the
high-temperature reservoir (q) is referred to as the efficiency of a heat engine. No heat engine, no matter how well constructed, can convert all the heat from the high-temperature reservoir into work.
Such an engine would be 100% efficient.
Sadi Carnot was the first scientist to realise this and deduce an expression showing the limitations of heat engines.
THE CARNOT CYCLE
In 1824 Sadi Carnot proposed a theoretical heat which could perform a series of operations and at the end of these operations the system was restored to the original state.
Statement: This cycle of processes which occurred under reversible conditions is referred to as the Carnot cycle.
The medium employed in operating Carnot’s engine was one mole of an ideal gas which could be imagined to be contained in a cylinder fitted with a frictionless piston.
Figure: Indicator diagram of the Carnot cycle.
The Carnot cycle comprises four operations or processes. They are,
(1) Isothermal reversible expansion (A→B)
(2) Adiabatic reversible expansion (B→C)
(3) Isothermal reversible compression (C→D)
(4) Adiabatic reversible compression (D→A)
First Operation – Isothermal Reversible Expansion
Let T2, P1 and V1 be the temperature, pressure and volume respectively of the gas enclosed in the cylinder initially. The cylinder is placed in the heat reservoir at the higher temperature (T2).
Now the gas is allowed to expand isothermally and reversibly so that the volume increases from V1 to V2.
Work done: Since the process in operation one is isothermal, thus, ΔE = 0.
According to the first law we know that, ΔE = q – w
or, 0 = q – w
or, w = q
or, q = w
If q2 be the heat absorbed by the system and w1 the work done by it, then we get
q2 = w1
Second Operation – Adiabatic Reversible Expansion
Let, the gas at B is at a temperature T2 and has volume V2 under the new pressure P2. The gas is now allowed to expand reversibly from volume V2 to V3 when the temperature drops from T2 to T1.
Work done: Since this step is adiabatic, thus; q = 0.
According to the first law we know that, ΔE = q – w
or, ΔE = 0 – w
or, ΔE =– w
If w2 be the work done, then we have
ΔE = – w2
or w2 = – ΔE
But ΔE = Cv (T1 – T2)
Therefore, w2 = Cv (T2 – T1) ……………………....(2)
Third Operation – Isothermal Reversible Compression
Now the cylinder is placed in contact with a heat reservoir at a lower temperature, T1. The volume of the gas is then compressed isothermally and reversibly from V3 to V4.
Work done: Since the process takes place isothermally, thus, ΔE = 0.
According to the first law we know that, ΔE = q – w
or, 0 = q – w
or, w = q
or, q = w
If q1 is the heat given to the reservoir and w3 the work done on the gas, we have
–q1 = –w3 (using proper signs for q and w)
Fourth Operation – Adiabatic Reversible Compression
The gas with volume V4 and temperature T1 at D is compressed adiabatically and reversibly and the volume of the system becomes V4 to V1 and its temperature T2.
Work done: In this step work is done on the system(gas) and, therefore, bears the negative (–) sign.
If it is denoted by w4, we can write
– w4 = – Cv (T2 – T1)…………………………………(4)
Net Work Done in One Cycle
Adding up the work done (w) in all the four operations of the cycle as shown in equations (1), (2), (3) and (4), we have
w = w1 + w2 + (– w3) + (– w4)
Net Heat Absorbed in One Cycle
Let, q is the net heat absorbed in the whole cycle.
Then we get, q = q2 – q1
Where q2 is heat absorbed by the system in operation one and q1 is the heat transferred to the sink reservoir in operation three.
From equations (1) and (3) we have
q = q2 – q1
According to the expression governing adiabatic changes,
Therefore, substituting the value of V3/V4 in equation (5), the value of net heat may be given as
Calculation of Thermodynamic Efficiency
Since the total work done in a cycle is equal to net heat absorbed, from (6) we can write
The heat absorbed, q2, at higher temperature T2 is given by equation (1),
Dividing equation (7) by (8) we get,
The factor w/q2 is called thermodynamical efficiency.
Free Energy
Two new thermodynamic properties that is the Gibbs free energy G, and Helmholtz free energy or work function A have recently been introduced.
The heat content of a system is divided into two parts. They are
Internal energy
External energy
From the first law of thermodynamics
H = E + PV
Total Energy Internal Energy External Energy
The total energy of external energy can be divided into two terms. They are
H = G + TS
Total Energy Free Energy Isothermally unavailable energy
Isothermally available energy
Finally the internal energy can be divided into the following two types
E = A + TS
Internal Energy Isothermally available energy Isothermally unavailable energy
A number of relations may obtain by rearranging these equations. As
Helmholtz free energy or work function A,
A=E–TS
and the Gibbs free energy G,
G=H–TS
or, G=E+PV–TS (Since, H=E+PV)
or, G=A+PV (Since, A=E–TS)
Thus it can be stated that, Gibbs free energy is the sum of Helmholtz free energy and PV work.
Pressure and Temperature Coefficients of Free Energy
The definition of the Gibbs energy can also be written as
G=E+PV–TS----------------------------------------------------------------(1)
By Applying the differential of a product, d(uv) = u dv + V du, to equation (1), we obtain the following relationship:
dG=dE+PdV+VdP–TdS–SdT--------------------------------------(2)
Since it is reversible process, So qrev=TdS
From the first law, we can write
dE= qrev –P.dV (Since, ΔE=q – w and w=PdV)
or, dE=TdS–PdV (Change of energy)
Now, substituting the value of dE) into equation (2) we get
dG=TdS–PdV+PdV+VdP–TdS–SdT
or, dG=VdP–SdT----------------------------------------------------(3)
There are two terms that can be derived. If the temperature is constant then dT=0 & Thus SdT=0 and equation (3) reduces to
dG=VdP
When the pressure is constant, then dP=0 Thus VdP=0 and equation (3) reduces to
dG=–SdT
To obtain the isothermal change of free energy, we integrate equation dG=VdP between states 1 and 2 at constant temperature:
For an ideal gas, the volume V is equal to nRT/P, thus allowing the equation 6 to be integrated:
Where ΔG is the free energy change of an ideal gas undergoing an isothermal reversible or irreversible alteration.
Gibbs-Helmholtz Equation
For an isothermal process at constant pressure preceding between the initial and final stages the equation can be written as
G2–G1=(H2–H1) –T(S2–S1)
or, ΔG=ΔH–TΔS
or, ΔG=ΔH+T(–ΔS)---------------------------------------------------(1)
We know, ( Now, equation (5) may be written as)
–ΔS=–(S2–S1)
Substituting the value of –ΔS in the equation 1we get,
This is one form of Gibbs –Helmholtz equation.
Get the Power Point Slides
Slide Share Link:
Watch Video Tutorials
Software Help